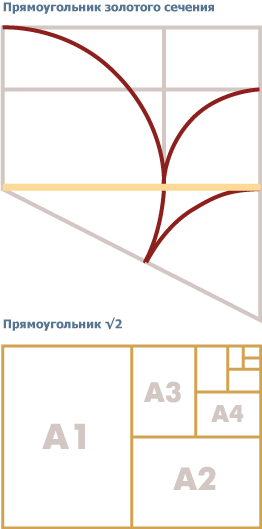Благодаря изначальному родству человека с природой он всегда формировал свой мир, интуитивно руковод­ствуясь чувством пропорции. Математика началась со счёта предметов и измерения пространства, художе­ственное конструирование — с размещения предметов относительно друг друга и окружающего пространства. Связь математики с конструированием прослеживает­ся с самых ранних цивилизаций. На протяжении всей истории человечества наука и искусство неоднократно объединялись в поисках наиболее совершенных форм художественной экспрессии.

Сетками пользуются для составления планов строи­тельства, разбивки территорий или украшения плоских поверхностей. Словари определяют сетку как «пере­плетение» равномерно расположенных горизонтальных и вертикальных линий, предназначенных для разме­щения точек по системе координат. С помощью сеток художники Возрождения увеличивали свои эскизы и использовали картоны при выполнении стенных росписей. Сетки — основа картографии, много веков по координатным сеткам составляются военные планы. Архитекторы-классики применяли сетки для вычерчивания перспектив в определенном масштабе. Со времен Гутенберга печатники пользовались сетка­ми для проектирования шрифта и верстки печатной страницы.

Сетка дизайнера в отличие от обычных макетных листов строится с учетом определенных пропорций и служит решению задач художественного конструи­рования. Придать материалу форму, соответствующую эстетическим критериям оценки конструкции, дизайнер может, во-первых, руководствуясь врожденным, интуитивным чувством пропорции, во-вторых, приме­нив один из принципов пропорционирования, раз­работанных в прошлом математиками, художниками­ – оформителями или архитекторами. Большинство дизайнеров предпочитают полагаться на интуицию, в то время как правильно организовать пространство на макете и создать качественную конструкцию без знания принципов пропорционирования нельзя. Поэто­му исследование сетки и систем модульного конструи­рования мы предваряем кратким обзором некоторых наиболее из них распространенных.

К тому времени, когда цивилизация, распространяясь через Эгейское море, достигла кульминации в Афин­ском Акрополе, уже сложились определенные эстетиче­ские принципы пропорционирования. Главный проектировщик Акрополя Фидий и архитектор Парфенона Иктин продемонстрировали знание тех возможностей, которые предоставляет деление линий в крайнем и среднем отношении. Этот способ деления пространства известен теперь как «золотое сечение». Одно из наиболее ранних определений структуры эстетической формы мы находим в книге Луки Пачоли «О божественной пропорции» (1509 г.). Эта пропорция точно может быть выражена делением отрезка так, чтобы меньшая часть относилась к большей, как эта большая ко всему отрезку. Если это деление продолжать, числа, выражающие длины отрез­ков, образуют ряд Фибоначчи (названный так по име­ни математика XIII в. из Пизы), в котором каждое последующее число равно сумме двух предыдущих.

Золотое сечение
Этот ряд отношений основан на правильном пятиуголь­нике, который вместе с вписанным в него правильным звездчатым многоугольником образует десятки золотых сечений. Прямоугольником золотого сечения называ­ется такой прямоугольник, короткая сторона которого равна наибольшему сечению его длинной стороны. Для дизайнеров с математическим складом ума отношение величин при золотом сечении выражается постоянным иррациональным числом 1,61803398, обозначаемым греческой буквой Ф — по первой букве имени греческого скульптора Фидия. Алгебраически это записывается обычно так: a:b=b:(a+b).

Квадрат
Золотое сечение — не единственный способ получения гармоничных пропорций. Важную роль при делении пространства имеют некоторые сочетания, основан­ные на простом квадрате. Из квадрата, являющегося естественной частью прямоугольника золотого сече­ния, может быть построен прямоугольник v2, который образуется проведением дуги радиусом, равным диагонали квадрата. Этот прямоугольник иногда путают с прямоугольником золотого сечения. Возможно, путаница произошла по вине группы кубистов, исполь­зовавших прямоугольник v2 назвавших свою выставку 1912 г. в Париже La Section d'Or («Золотое сечение»). Этот прямоугольник составляет основу для форматов серии А принятой в качестве стандарта в Европе и Ве­ликобритании. Самый распространенный А4 (210?297 мм). Квадрат также играет ключевую роль в модуль­ной системе японского национального дома, которая исходит от размера соломенных циновок — «татами». Пропорция двойного квадрата соломенных циновок размером приблизительно 3х6 футов (0,91?1,83 м) делила площадь пола на различные залы, что созда­вало удивительное разнообразие асимметричных форм в традиционных японских домах. Простейший прямоугольник, квадрат, был, пожалуй, для современ­ных дизайнеров более важным фактором в развитии сетки, чем золотое сечение или любая другая система пропорций. Дизайнер, приступая к изго­товлению макета квадратного формата, сталкивается с необычайно ценной практикой, несмотря на то, что эта форма неэкономична, а для большинства случаев и неудобна.

1 2 3